Method and System for learning behaviour of highly complex and non-linear systems - Complexity Based Oracle Sampling

Non-Linear Complex simulations of physical systems using the laws of physics such as thermodynamics, chemical reactions, differential equations etc. are simulated to solve for a given input. These simulations are time-taking and are unfeasible to run multiple times for the entire operational range in business situations. Using Linear Approximation of the complex simulations helps in faster results generation with acceptable errors, it is less accurate but quick to do and works only far a small range of input domain. Neural Networks once trained enough can approximate these input-output mapping better than Linear Approximations and can give simulation results faster than traditional simulation algorithms. Neural Networks can be trained in two ways:

1. Using pre-collected dataset
2. By sampling mathematical models which can simulate physical systems

For training Neural Networks to approximate a black-box model, the simulation dataset needs to be sampled using a black-box model, or via an Oracle function which can efficiently simulate the given physical system. This sampling needs to be optimized in such a way that more data is sampled where the complexity of the manifold is high, while keeping the number of total data points sampled at minimum. Curriculum Learning is a classic learning strategy which states that learning algorithms can be trained in an efficient manner by gradually exposing the algorithm to difficult or complex data points with iterations. We propose an iterative training approach which starts with a coarse level dataset and iteratively employs a curriculum learning strategy to sample highly complex data points.

Claims:

1. Proposes a complexity-based sampling methodology to train Neural Network via an oracle function
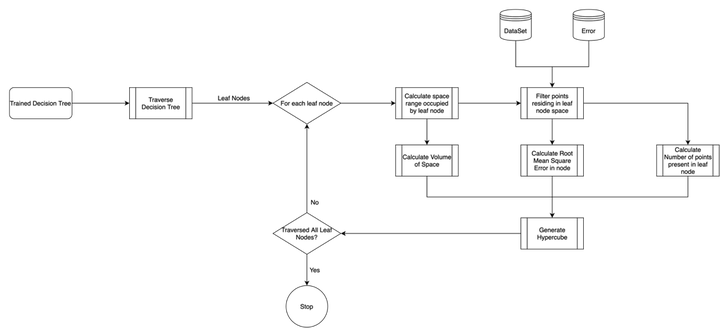
2. The algorithm samples points proportional to the complexity of a region in an iterative fashion, while training a neural network.
3. For finding pure regions of near constant complexity, a regression tree is used. Same function can also be achieved by other methods that divide the space based on a criteria, such as KD Trees.
4. Complexity is defined by the accuracy of the trained neural network in a given region during an iteration.
5. Data generated is weighed in proportion to its iteration number while training the neural network, to avoid excessive overfitting.
6. The network is trained until a threshold of accuracy is reached on the testing dataset.
7. Proposed method performs Iterative Curriculum Sampling.